ANOVA for Categorical

We can use the f-distribution for ANOVAs (Analysis of Variance), which we’ve seen can be used to compare models, but they are also great for categorical variables.

A linear model with only categorical predictors have traditionally been called analysis of variance (ANOVA). The purpose is to find whether statistically significant differences exist between the means of several independent groups.

One-Way ANOVA

  • \(H_0\): \(\mu_A = \mu_B = \mu_C = \dots\) for all groups/categories (i.e. the means of each group are the same)
  • \(H_a\): at least one of the groups/categories’ means differ from the rest (i.e. at least one pair of means is not equal, or at least one sample mean is not equal to the others)

We want to compare the global mean to all sub-means.

  • Global: \(\frac{\sum \text{Values}}{\sum \text{Group Sizes}}\)
  • Group Means: \(\bar{y_i}\)

We can variance in the data by the following:

  • Total Sum of Squares: \(SST = \sum\limits_{i=1}^{I} \sum\limits_{j=1}^{n_i} (y_{ij} - \bar{\bar{y}})^2\)
    • \(i \in {1, \dots, I}\): group/category
    • \(j \in {1, \dots, n_i}\) value within group/category
  • Within-Group Sum of Squares: \(SSW = \sum\limits_{i=1}^{I} \sum\limits_{j=1}^{n_i} (y_{ij} - \bar{y_i})^2\)
    • how much groups are split from their own mean
  • Between-Group sum of Squares: \(SSB = \sum\limits_{i=1}^{I} \sum\limits_{j=1}^{n_i} (\bar{y_i} - \bar{\bar{y}})^2\)
    • how much groups are split from the total mean
  • \(SST = SSW + SSB\)
    • goal: we want to know which term dominates between \(SSW\) and \(SSB\)

Allowing for each group to have its own means accounts for \(\frac{SSB}{SST}\) percent of the variability. This is very similar to an \(R^2\).

Degrees of Freedom

Given \(I\) number of groups/categories and \(N\) total number of data points (across all groups/categories; recall that groups can have different number of data points):

  • \(SSB_{df} = I-1\)
  • \(SSW_{df} = N-I\)

F-Statistic

Given:

  • \(H_0\): \(\mu_0 = \mu_1 = \mu_2\)
  • \(H_a\): \(\mu_i \neq \mu_j\) for some pair \(i, j\)

\(F_{stat} = \frac{SSB/SSB_{df}}{SSW/SSW_{df}} = \frac{\frac{SSB}{I-1}}{\frac{SSW}{N-I}}\)

Rejection Region: \(F_{\alpha,I-1,N-I}\)

ANOVA Table

It’s common to summarize everything associated with the analysis of variance in a table.

Given the example:

Control Diet A Diet B
3 5 5
2 3 6
1 4 7
ANOVA SS DF SS/DF \(F_{stat}\)
between 24 2 12 12
within 6 6 1
between 30

ANOVA as MLR

\(y = Control + \text{Effects of Groups} + Errors\)

A point in group \(i\) would look like:

\(y = \beta_0 + beta_i + \epsilon\)

We use indicator variables to set this up:

\(x_{ij} = \begin{cases} 1 \\ 0 \end{cases}\)

We choose one group as control and create the model:

\(y_{ij} = \mu_0 + \tau_1 x_{1j} + \tau_2 x_{2j} + \dots + \tau_{I-1} x_{{I-1}, j} + \epsilon_{ij}\)

where \(y_{ij}\) is the \(j^{th}\) response for the \(i^{th}\) group

Recall our example:

Control Diet A Diet B
3 5 5
2 3 6
1 4 7
\(y_{ij}\) \(y_{1j}\) \(y_{2j}\)
3 0 0
2 0 0
1 0 0
5 1 0
3 1 0
4 1 0
5 0 1
6 0 1
7 0 1

Tukey’s Honest Significance Test

The F-test gives us a single conclusion on a model like this: groups matter. It doesn’t tell us how much or which groups matter. To answer this, we have to resort to more individual tests, like testing group A against group B, group A against the control, and group B against the control.

However, this sets us up for Type I Errors.

Given an error probability of \(\alpha\), what is the total probability we commit an error?

\(P(\text{no error}) = \prod\limits_{i=1}^{I} P(\text{no error}_i) = (1-\alpha)^i\)

Therefore,

\(P(error) = 1 - (1-alpha)^i\)

If we have 3 features and a set error rate of \(alpha = 0.05\),

\(P(error) = 1 - (0.95)^3 \approx 0.14\)

In summary, \(\alpha\) for the F-statistic tells us groups matter. If and only if the F-statistic is significant, we can perform a careful version of pairwise testing between groups that accounts for both the fact that we’re doing multiple tests and that those tests aren’t independent.

The Test

Suppose we determine that some of the means are different. How can we tell which ones?

Tukey’s Honest Significance Test (HST/HSD) post-hoc test for iff we reject the null hypothesis

  • Hypothesis test for pairwise comparison of means: many tests using what’s called the studentized range distribution
  • Adjusts so that the probability of making a Type I error over all possible pairwise comparisons is kept at the original \(\alpha\)

We can draw a conclusion from both the confidence interval and p-values output from this method (given a prescribed \(\alpha\).

  • confidence interval [lower bound, upper bound]: if the lower bound and upper bound do not contain \(0\), we know that the difference between these groups is significant. In particular, we can know if the difference is positive, since the lower bound of the confidence interval is greater than \(0\).
  • p-value: given a confidence interval which does not contain \(0\), we would likely see a small enough p-value to reject the null hypothesis, indicating that the difference between the groups’ means is statistically significant.

In other words, we’d be doing the same test as before, just pairwise:

  • \(H_0\): \(\mu_i = \mu_j = \mu_C = \dots\) for two groups/categories \(i, j\)
  • \(H_a\): \(\mu_i \neq \mu_j\) for two groups/categories \(i, j\)

Implementation

Import Libraries

Code 
Warning: package 'car' was built under R version 4.3.3
Warning: package 'carData' was built under R version 4.3.3

Creating the Dataset

Code
Control = c(3, 2, 1)
DietA = c(5, 3, 4)
DietB = c(5, 6, 7)

df = data.frame(Control,DietA,DietB)
df
  Control DietA DietB
1       3     5     5
2       2     3     6
3       1     4     7

Put into Long Format

Code
longdata <- gather(df, group, value)
longdata
    group value
1 Control     3
2 Control     2
3 Control     1
4   DietA     5
5   DietA     3
6   DietA     4
7   DietB     5
8   DietB     6
9   DietB     7

One-Way ANOVA Test

Perform Oneway ANOVA Test (var.equal = TRUE for this test, Var.equal = FALSE is another test)

Code
result <- oneway.test(value ~ group, data = longdata, var.equal = TRUE)

The Results

Code
Fstat = result$statistic
pvalue = result$p.value

Fstat
 F 
12
Code
pvalue
[1] 0.008

ANOVA as MLR

We get a low enough p-value that we have enough evidence to reject the null hypothesis and conclude that at least one mean is different.

What about the idea that ANOVA F-test is equivalent to linear regression where the features are binary categorical variables associated with group membership. We can recreate the 0, 1 dataframe.

Code
# x1: indicates membership in diet a
# x2: indicates membership in diet b

x1 <- as.integer(longdata$group == 'DietA')
x2 <- as.integer(longdata$group == 'DietB')
y <- longdata$value

y
[1] 3 2 1 5 3 4 5 6 7
Code
x1
[1] 0 0 0 1 1 1 0 0 0
Code
x2
[1] 0 0 0 0 0 0 1 1 1
Code
dfRegression <- data.frame(y, x1, x2)
dfRegression
  y x1 x2
1 3  0  0
2 2  0  0
3 1  0  0
4 5  1  0
5 3  1  0
6 4  1  0
7 5  0  1
8 6  0  1
9 7  0  1

Perform MLR and compare the computed F-test

Code
anova_regression <- lm(y ~ ., data = dfRegression)
summary(anova_regression)

Call:
lm(formula = y ~ ., data = dfRegression)

Residuals:
   Min     1Q Median     3Q    Max 
    -1     -1      0      1      1 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)   2.0000     0.5774   3.464  0.01340 * 
x1            2.0000     0.8165   2.449  0.04983 * 
x2            4.0000     0.8165   4.899  0.00271 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1 on 6 degrees of freedom
Multiple R-squared:    0.8, Adjusted R-squared:  0.7333 
F-statistic:    12 on 2 and 6 DF,  p-value: 0.008

Analysis of Variance Summary Table

Use aov() to create a summary table from original long data

Code
weightloss_study_aov <- aov(value ~ group, data = longdata)
summary(weightloss_study_aov)
            Df Sum Sq Mean Sq F value Pr(>F)   
group        2     24      12      12  0.008 **
Residuals    6      6       1                  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Tukey Test

Use TukeyHSD() on the aov summary to test which weight loss group(s) are statistically different

Code
# NOTE: can set significance level, i.e. TukeyHSD(aov_model, conf.level=0.95)
tukey_test <- TukeyHSD(weightloss_study_aov)
tukey_test
  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = value ~ group, data = longdata)

$group
              diff        lwr      upr     p adj
DietA-Control    2 -0.5052356 4.505236 0.1088670
DietB-Control    4  1.4947644 6.505236 0.0064937
DietB-DietA      2 -0.5052356 4.505236 0.1088670

Plotting the Tukey Test Results

Code
plot(tukey_test)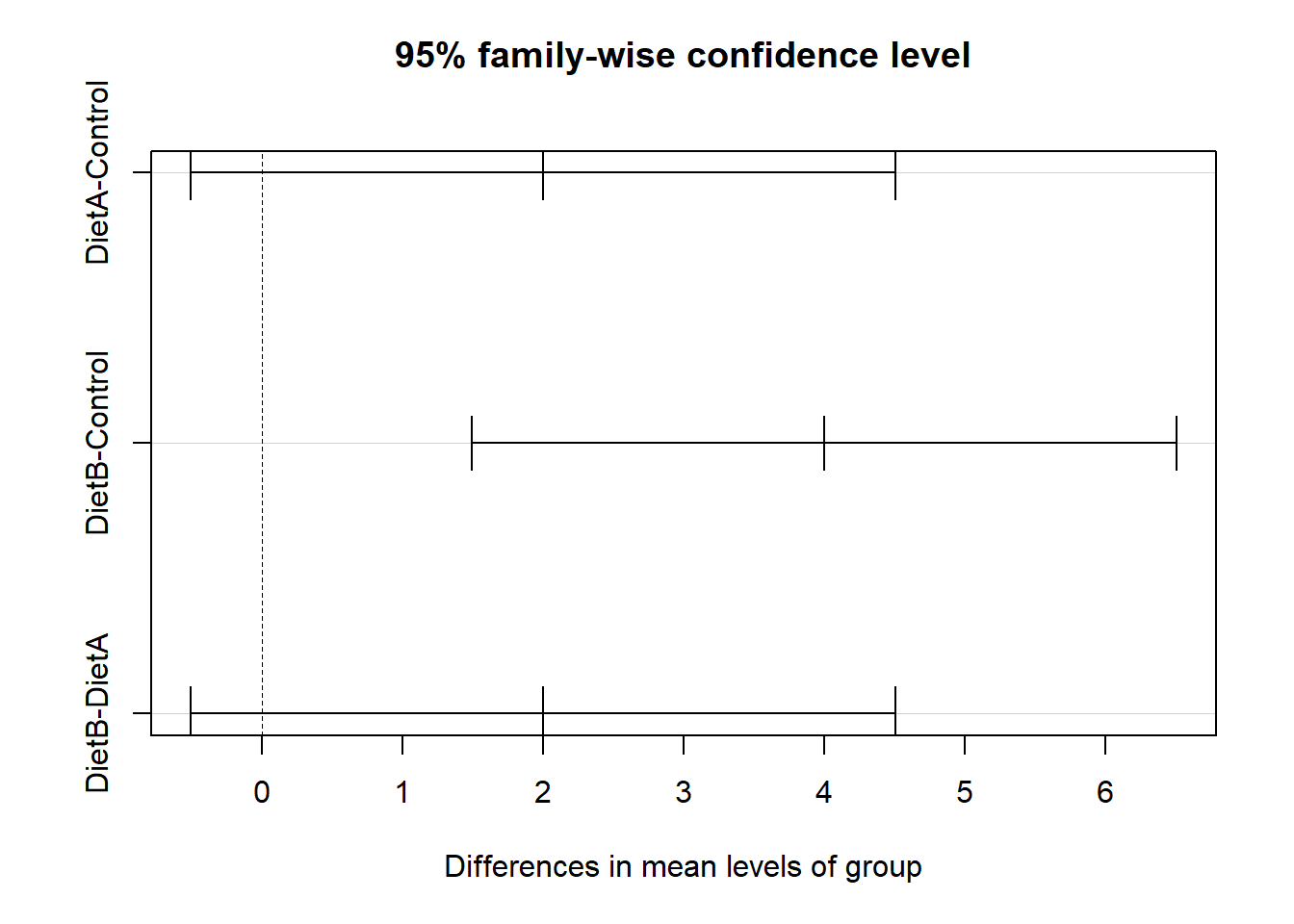

Checking Assumptions

Specifically, we want to check:

  • homogeniety of variance assumption
  • normality assumption

Plotting

Code
plot(weightloss_study_aov)

Levenes’ Test (constant variance)

Code
leveneTest(value ~ group, data = longdata)
Warning in leveneTest.default(y = y, group = group, ...): group coerced to
factor.
Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  2       0      1
       6
  • \(H_0\): homogeneity of variance across all groups
  • \(H_a\): homogeneity of variance condition violated

Shapiro-Wilk’s test (normality)

Code
aov_residuals <- residuals(object = weightloss_study_aov)
shapiro.test(x = aov_residuals)

    Shapiro-Wilk normality test

data:  aov_residuals
W = 0.82304, p-value = 0.03729

What if Assumptions are not Met?

When assumptions are not met, we can use a non-parametric test known as the Kruskal-Wallis rank sum test, which determines whether or not there is a statistically significant difference between the medians of three or more independent groups. Note this returns a chi-squared value.

  • \(H_0\): the median is equal across all groups
  • \(H_a\): the median is not equal across all groups
Code
kruskal.test(value ~ group, data = longdata)

    Kruskal-Wallis rank sum test

data:  value by group
Kruskal-Wallis chi-squared = 6.5311, df = 2, p-value = 0.03818

We can further determine which groups have significant differences between them by using pairwise.wilcox.test().