Cluster Analysis

Considerations for Cluster Analysis

• Partitioning Criteria:
  • single level
  • hierarchical partitioning
  • often, multi-level hierarchical partitioning is desirable, i.e. grouping topical terms
• Separation of Clusters:
  • Exclusive: one customer belongs to only one region
  • Non-Exclusive: one document may belong to more than one clas
• Similarity Measure:
  • Distance-Based: Euclidean, road network, vector
  • Connectivity-Based: density or contiguity
• Clustering Space:
  • Full Space: often when low dimensional
  • Subspaces: often in high dimensional clustering

Requirements & Challenges

• Quality:
  • ability to deal with different types of attributes
    • numerical
    • categorical
    • text
    • multimedia
    • networks
    • mixture of multiple types
• Scalability:
  • clustering all the data instead of only on samples
  • high dimensionality
  • incremental or stream clustering and insensitivity to input order
• Constraint-Based Clustering:
  • user-given preferences or constraints
  • domain knowledge
  • user queries
• Interpretability and Usability

Major Clustering Methods

• Partitioning Methods:
  • construct k partitions
  • iterative relocation
• Hierarchical Methods:
  • hierarchical decomposition
  • split/merge
• Density-Based Methods:
  • connectivity
  • density functions
• Grid-Based Methods:
  • quantize into cells
  • multi-granuality grid
• Model-Based Methods:
  • hypothesized cluster model
  • best fit
• Clustering High-Dimensional Data
  • subspace clustering
  • frequent-pattern-based clustering
• Constraint-Based Clustering
  • user-specified
  • application-oriented constraints

Partitioning Methods

• Given a data set D of n objects
• Given k, find a partition of k clusters that optimizes the chosen partition criterion
• Global optimal: enumerate all partitions
• Heuristic methods:
  • K-Means: cluster represented by mean (centroid)
  • K-Medoids: cluster represented by medoid (object closest to centroid)
• Partitioning method: discovering the groupings in the data by optimizing a specific objective function and iteratively improving the quality of partitions
• K-partitioning method: partitioning a dataset D of n objects into a set of K clusters so that an objective function is optimized (i.e. sum of squared distances is minimized, where \(c_K\) is the centroid of cluster \(C_k\))
  • a typical objective function: sum of squared errors (SSE): \(SSE(C) = \sum\limits_{k=1}^K \sum\limits_{x_i \in C_k} |x_i - c_k|^2\)
• Problem definition: given K, find a partition of K clusters that optimizes the chosen partitioning criterion
  • global optimal: needs to exhaustively enumerate all partitions
  • heuristic methods (i.e. greedy algorithms):
    • K-Means
    • K-Medoids
    • K-Medians
    • etc.

K-Means Clustering

Algorithm

• Partition objects into k nonempty clusters
• Compute the mean (centroid) of each cluster
• Assign each object to the closest centroid
  • closest depends on the distance measurement used (i.e. Euclidean, Manhattan, etc.)
• Repeat until there are no more assignment changes

Discussion

• Efficiency: \(O(tKn)\)
  • n: number of objects
  • K: number of clusters
  • t: number of iterations
  • normally, \(K, t << n\)
• K-means clustering often terminates at a local optimum (initialization can be important to find high-quality clusters)
• Need to specify K, the number of clusters, in advance
  • there are method to automatically determine the “best” K
  • in practice, we often run a range of values and select the “best” K value
• Sensitive to Noisy Data and Outliers
  • K-medians, K-medoids, etc. can be better equipped to handle outliers
• K-means applies only to objects in a continuous n-dimensional space
  • using the K-modes for categorical data
• Not suitable to discover clusters with non-convex shapes
  • more suitable methods are using density-based clustering, kernel K-means, etc.
• Further Variations of K-Means
  • Choosing better initial centroid estimates
    • K-means++, Intelligent K-Means, Genetic K-Means
  • Choosing different representative prototypes for clusters
    • K-Medoids, K-Medians, K-Modes
  • Applying feature transformation techniques
    • Weighted K-Means, Kernel K-Means

K-Medoids Clustering

• PAM (partitioning around medoids)
  • starts from an initial set of medoids
  • iteratively replace a medoid with a non-medoid if it reduces the total distance
  • effective for small data sets, does not scale, \(O(k(n-k)^2)\) for each iteration
• CLARA: apply PAM only multiple sampled sets
• CLARANS: use randomized samples to search for neighboring solutions

Discussion

• K-Medoids Clustering: find representative objects (medoids) in clusters
• PAM
  • starts from an initital set of medoids
  • iteratively replaces one of the medoids by one of the non-medoids if it improves the total sum of squared errors (SSE) of the resulting clustering
  • PAM works effectively for small data sets but does not scale well for large data sets (due to the computational complexity)
• Efficiency Improvements on PAM:
  • CLARA: PAM on samples
  • CLARANS: randomized re-sampling, ensuring efficiency & quality

Elbow Method

• heuristic used to determine the optimal number of clusters (k) for a clustering algorithm, such as K-Means
• involves plotting the within-cluster sum of squares WCSS for a range of k values and looking for an “elbow” point on the graph
• mathematical elbow: the point where the rate of decrease in WCSS sharply changes is a good choice for the number of clusters

wcss = [] # within-cluster sum of squares
for i in range(1, 11):
  model = KMeans(n_clusters = i)
  y_kmeans = model.fit_predict(x)
  wcss.append(model.intertia_) # adding accuracy to our model

Hierarchical Clustering

• Basics
  • generate a clustering hierarhcy (drawn as a dendrogram)
  • not required to specify K, the number of clusters
  • more deterministic
  • no iterative refinement
• Two Categories of Algorithms
  • agglomerative: start with singleton clusters, continuously merge two clusters at a time to build a bottom-up hierarchy of clusters
  • divisive: start with a huge macro-cluster, split it continuously into two groups, generating a top-down hierarchy of clusters

Dendrogram: How Clusters are Merged

• Dendrogram: decompose a set of data objects into a tree of clusters by multi-level nested partitioning
• A clustering of the data objects is obtained by cutting the dendrogram at the desired level, then each connected components forms a cluster

Agglomerative Clustering Algorithm

• AGNES (AGglomerative NESting)
  • use single-link method and the dissimilarity matrix
  • continuously merge nodes that have the least dissimilarity
  • eventually all nodes belong to the same cluster
• Agglomerative clustering varies on different similarity measures among clusters
  • single link (nearest neighbor)
  • complete link (diameter)
  • average link (group average)
  • centroid link (centroid similarity)

Single Link vs. Complete Link in Hierarhcical Clustering

Single Link (nearest neighbor)

• similarity between two clusters is the similarity between their most similar (nearest neighbor) members
• local similarity-based: emphasizing more on close regions, ignoring the overall structure of the cluster
• capable of clustering non-elliptical shaped group of objects
• sensitive to noise and outliers

Complete Link (diameter)

• similarity between two clusters is the similarity between their most dissimilar members
• merge two clusters to form one with the smallest diameter
• nonlocal in behavior, obtaining compact shaped cluster
• sensitive to outliers

Agglomerative

• each observation starts in its own cluster
• clusteres are successively merged together
• linkage criteria determines merge strategy
  • ward: minimize the sum of squared differences within clusters
  • max/complete: minimize the max distance within clusters
  • average: minimize the average distance within clusters
  • single: minimize the minimal distance within clusters

Feature Agglomerative

• Feature Agglomerative uses agglomerative clustering to group together features that look very similar, thus decreasing the number of features
• dimensionality reduction tool

Implementation (sklearn)

Import Libraries and Make Data

# libraries
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# data
x, y = make_blobs(n_samples=100,
                  centers=4, n_features=2,
                  cluster_std=[1,1.5,2, 2],
                  random_state=7)
                  
# make blobs
df_blobs = pd.DataFrame({
    'x1': x[:,0],
    'x2':x[:,1],
    'y':y

})

df_blobs.head()

	x1	x2	y
0	-3.384261	5.221740	1
1	-1.836238	-7.735384	3
2	-7.456176	6.198874	0
3	-1.785043	1.609749	1
4	-10.124910	6.133805	0

2-D Plot Function

def plot_2d_clusters(x, y, ax):
    y_uniques = pd.Series(y).unique()

    for cl in y_uniques:
        x[y==cl].plot(
            title=f'{len(y_uniques)} Clusters',
            kind='scatter',
            x='x1',
            y='x2',
            marker = f'${cl}$',
            ax = ax
        )

First Image

fig, ax = plt.subplots(1,1, figsize=(15,10))
x, y = df_blobs[['x1','x2']], df_blobs['y']
plot_2d_clusters(x,y,ax)

Applying Clustering

kmeans = KMeans(n_clusters=100, random_state=7)
y_pred = kmeans.fit_predict(x)

C:\Users\carlj\anaconda3\lib\site-packages\sklearn\cluster\_kmeans.py:1412: FutureWarning:

The default value of `n_init` will change from 10 to 'auto' in 1.4. Set the value of `n_init` explicitly to suppress the warning

C:\Users\carlj\anaconda3\lib\site-packages\sklearn\cluster\_kmeans.py:1436: UserWarning:

KMeans is known to have a memory leak on Windows with MKL, when there are less chunks than available threads. You can avoid it by setting the environment variable OMP_NUM_THREADS=1.

fig, axs = plt.subplots(1, 2, figsize=(20,12))
plot_2d_clusters(x,y,axs[0])
plot_2d_clusters(x,y_pred,axs[1])

axs[0].set_title(f'Actual {axs[0].get_title()}')
axs[1].set_title(f'Kmeans {axs[1].get_title()}')

Text(0.5, 1.0, 'Kmeans 100 Clusters')

Test on Real Data

df = pd.read_csv('data/uber_clean.csv')
df.head()

	Date/Time	Lat	Lon	Base	Date
0	2014-07-01 0:03	40.7586	-73.9706	B02512	Tuesday
1	2014-07-01 0:05	40.7605	-73.9994	B02512	Tuesday
2	2014-07-01 0:06	40.7320	-73.9999	B02512	Tuesday
3	2014-07-01 0:09	40.7635	-73.9793	B02512	Tuesday
4	2014-07-01 0:20	40.7204	-74.0047	B02512	Tuesday

x = df[["Lat", "Lon"]] # features
x.head()

	Lat	Lon
0	40.7586	-73.9706
1	40.7605	-73.9994
2	40.7320	-73.9999
3	40.7635	-73.9793
4	40.7204	-74.0047

model = KMeans(n_clusters = 3)
y_kmeans = model.fit_predict(x)
df['y'] = y_kmeans  # store it in an actual frame
df.head()
plt.scatter(df['Lon'], df['Lat'], c=df['y']) # colorized based on y-values (clusters based on lat long k-means)

C:\Users\carlj\anaconda3\lib\site-packages\sklearn\cluster\_kmeans.py:1412: FutureWarning:

The default value of `n_init` will change from 10 to 'auto' in 1.4. Set the value of `n_init` explicitly to suppress the warning

Inertia

# model inertia: measures how well a data set was clustered by k-means

# meaure the distance between each data point and its centroid, square this distance, and sume up
# these squares across one cluster

# a good model is one with a low inertia value and low number of cluster (K)

model.inertia_

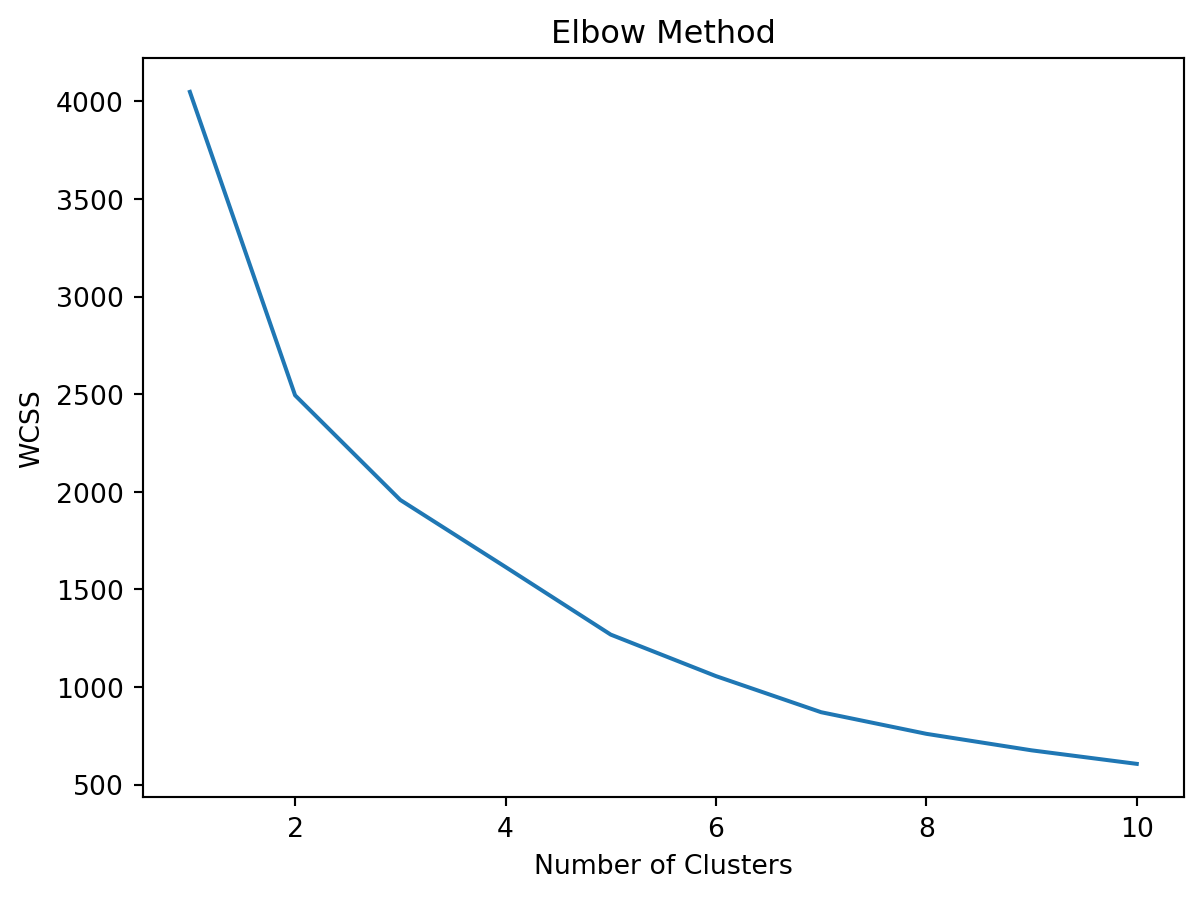
1957.7363841201532

Elbow Method

wcss = [] #  within-cluster sum of squares
for i in range(1,11):
    model = KMeans(n_clusters = i)
    y_kmeans = model.fit_predict(x)
    wcss.append(model.inertia_)  # adding accuracy to our model
    
plt.plot(range(1,11), wcss)
plt.xlabel('Number of Clusters')
plt.ylabel('WCSS')
plt.title('Elbow Method')
plt.show()

C:\Users\carlj\anaconda3\lib\site-packages\sklearn\cluster\_kmeans.py:1412: FutureWarning:

The default value of `n_init` will change from 10 to 'auto' in 1.4. Set the value of `n_init` explicitly to suppress the warning

C:\Users\carlj\anaconda3\lib\site-packages\sklearn\cluster\_kmeans.py:1412: FutureWarning:

The default value of `n_init` will change from 10 to 'auto' in 1.4. Set the value of `n_init` explicitly to suppress the warning

C:\Users\carlj\anaconda3\lib\site-packages\sklearn\cluster\_kmeans.py:1412: FutureWarning:

The default value of `n_init` will change from 10 to 'auto' in 1.4. Set the value of `n_init` explicitly to suppress the warning

C:\Users\carlj\anaconda3\lib\site-packages\sklearn\cluster\_kmeans.py:1412: FutureWarning:

The default value of `n_init` will change from 10 to 'auto' in 1.4. Set the value of `n_init` explicitly to suppress the warning

C:\Users\carlj\anaconda3\lib\site-packages\sklearn\cluster\_kmeans.py:1412: FutureWarning:

The default value of `n_init` will change from 10 to 'auto' in 1.4. Set the value of `n_init` explicitly to suppress the warning

C:\Users\carlj\anaconda3\lib\site-packages\sklearn\cluster\_kmeans.py:1412: FutureWarning:

The default value of `n_init` will change from 10 to 'auto' in 1.4. Set the value of `n_init` explicitly to suppress the warning

C:\Users\carlj\anaconda3\lib\site-packages\sklearn\cluster\_kmeans.py:1412: FutureWarning:

The default value of `n_init` will change from 10 to 'auto' in 1.4. Set the value of `n_init` explicitly to suppress the warning

C:\Users\carlj\anaconda3\lib\site-packages\sklearn\cluster\_kmeans.py:1412: FutureWarning:

The default value of `n_init` will change from 10 to 'auto' in 1.4. Set the value of `n_init` explicitly to suppress the warning

C:\Users\carlj\anaconda3\lib\site-packages\sklearn\cluster\_kmeans.py:1412: FutureWarning:

The default value of `n_init` will change from 10 to 'auto' in 1.4. Set the value of `n_init` explicitly to suppress the warning

C:\Users\carlj\anaconda3\lib\site-packages\sklearn\cluster\_kmeans.py:1412: FutureWarning:

The default value of `n_init` will change from 10 to 'auto' in 1.4. Set the value of `n_init` explicitly to suppress the warning

Visualize Data on a Map

# import folium
import folium

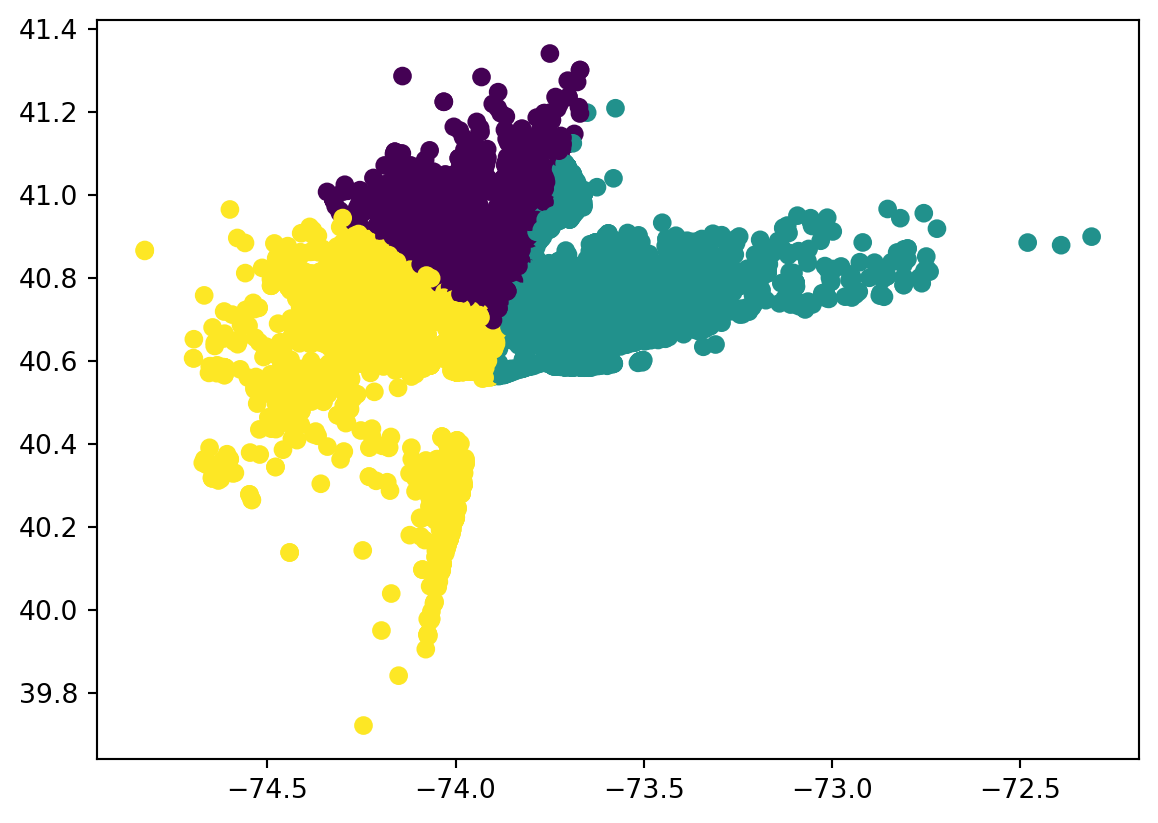
# visaulize data in actual map

df = df[:2000]  # instead of 40,000

clusters1  = df[['Lat', "Lon"]][df['y'] == 0].values.tolist()
clusters2  = df[['Lat', "Lon"]][df['y'] == 1].values.tolist()
clusters3  = df[['Lat', "Lon"]][df['y'] == 2].values.tolist()

# map
city_map = folium.Map(location= [40.7128, -74.0060], zoom_start = 10, titles = "openstreetmap")

for i in clusters1:
    folium.CircleMarker(i, radius =2, color = 'blue', fill_color = 'lightblue').add_to(city_map)

for i in clusters2:
    folium.CircleMarker(i, radius =2, color = 'red', fill_color = 'lightred').add_to(city_map)

for i in clusters3:
    folium.CircleMarker(i, radius =2, color = 'green', fill_color = 'lightgreen').add_to(city_map)
    
city_map

Make this Notebook Trusted to load map: File -> Trust Notebook